Video games are time-consuming. The problem is they’re fun, engrossing, often beautiful, and tell great stories. Beating them is also satisfying. Most people beat a game and are done with it. But for others the job is not done after defeating the final boss–they must go on to accomplish every task available. These poor people are called ‘completionists’.
It takes longer to complete a game than to merely beat it. But how much longer? And how can we model the relationship between time to beat and time to complete?
Getting the Data
There’s a lot of data on Twitter. Most of it is unstructured, nonsensical, and profane. One exception, however, is the HowLongToBeat account. Scroll through the tweets and you’ll notice a pattern:
It takes X hours on average to beat Y, (Z hours for completionists)
![]()
That’s (mostly) structured data! We just need {rtweet} and some regular expressions to extract the names and hours variables. Here’s one way:
library(rtweet)
library(gt)
library(stringr)
library(unglue)
library(tidyverse)
library(broom)
library(ggExtra)
library(ggtext)
library(ggalt)
library(hrbrthemes)
tobeat <- get_timeline("HowLongToBeat", n = 500)
tobeat <- tobeat %>% filter(grepl("It takes.*on average.*for completionists", text))
url_pattern <- "http[s]?://(?:[a-zA-Z]|[0-9]|[$-_@.&+]|[!*\\(\\),]|(?:%[0-9a-fA-F][0-9a-fA-F]))+"
imgs <- tobeat$text %>%
str_extract_all(url_pattern) %>%
map_dfr(set_names, c("img1", "img2"))
gametimes <- tibble(
name = tobeat$text %>% str_extract("(?<=beat )(.*)(?= \\()"),
hrs_to_beat = parse_number(tobeat$text %>% str_extract("\\d\\.?\\d?.*to beat")),
hrs_to_comp = parse_number(tobeat$text %>% str_extract("(?<=\\().*(?= hours for)"))
) %>%
bind_cols(imgs) %>%
arrange(name)
glimpse(gametimes)Rows: 29
Columns: 5
$ name <chr> "Animal Crossing: New Horizons", "Assassin's Creed IV: Black F…
$ hrs_to_beat <dbl> 60.5, 23.0, 43.0, 12.5, 46.0, 48.5, 9.0, 24.5, 2.0, 31.0, 22.5…
$ hrs_to_comp <dbl> 363.0, 59.5, 105.0, 33.5, 149.0, 192.0, 10.0, 60.0, 2.5, 82.0,…
$ img1 <chr> "https://t.co/vPZeL1V7sj", "https://t.co/IbCtFNfoHx", "https:/…
$ img2 <chr> "https://t.co/zdWE2Z77cg", "https://t.co/qk0RVyz0OC", "https:/…
Plotting the relative differences:
gametimes %>%
mutate(name = fct_reorder(name, hrs_to_comp)) %>%
ggplot(aes(x = hrs_to_beat, xend = hrs_to_comp, y = name)) +
geom_dumbbell(
color = "pink",
size = 1.5,
colour_xend = "steelblue",
dot_guide = TRUE,
dot_guide_size = 0.15
) +
labs(
x = "Hours",
y = NULL,
title = "Hours to Beat ~ Hours to Complete"
) +
theme_ipsum()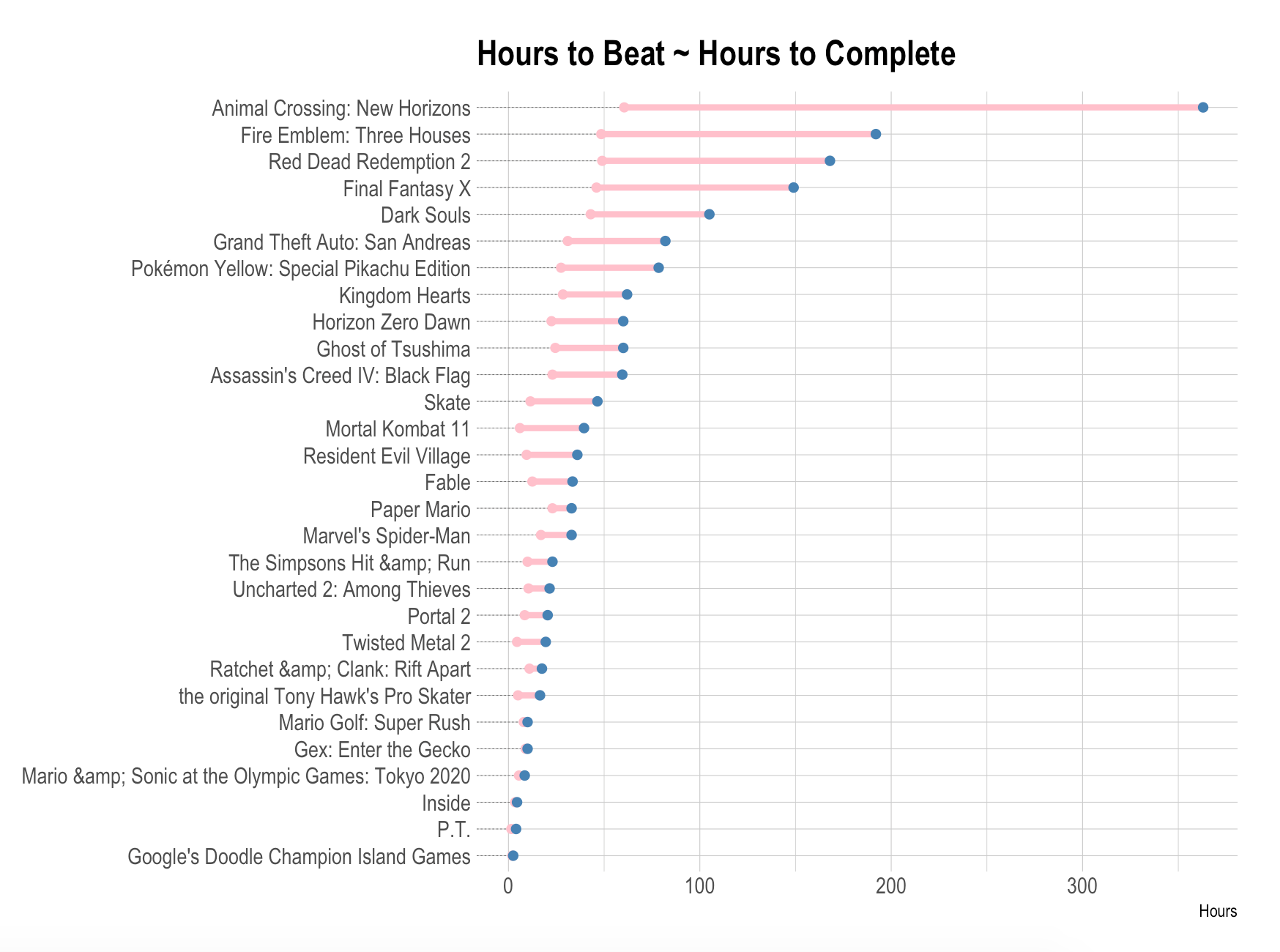
Obviously, the longer a game takes to beat, the longer it takes to complete. Let’s model the relationship:
with(gametimes, cor(hrs_to_comp, hrs_to_beat))
lm1 <- lm(hrs_to_comp ~ hrs_to_beat, data = gametimes)
summary(lm1)Call:
lm(formula = hrs_to_beat_comp ~ hrs_to_beat, data = gametimes)
Residuals:
Min 1Q Median 3Q Max
-55.332 -17.349 -2.289 16.042 128.886
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) -20.9602 10.8826 -1.926 0.066 .
hrs_to_beat 4.2161 0.4134 10.199 3.34e-10 ***
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 34.91 on 24 degrees of freedom
Multiple R-squared: 0.8125, Adjusted R-squared: 0.8047
F-statistic: 104 on 1 and 24 DF, p-value: 3.343e-10
While the metrics are great (high R-squared, low p-value, etc.), the model is problematic for several reasons. First, I have a limited number of observations (27). Second, Y is inseparably part of X–they are in some respect measures of the same thing. Third, Animal Crossing is a conspicuous outlier tilting the model’s fit. Its Cook’s D is enormous:
augment(lm1) %>%
ggplot(aes(.cooksd)) +
geom_dotplot() +
theme_ipsum() +
annotate(
"text",
x = 3, y = 0.025,
label = "Animal Crossing",
color = "firebrick"
) +
theme(
axis.title.y = element_blank(),
axis.text.y = element_blank(),
axis.ticks.y = element_blank()
)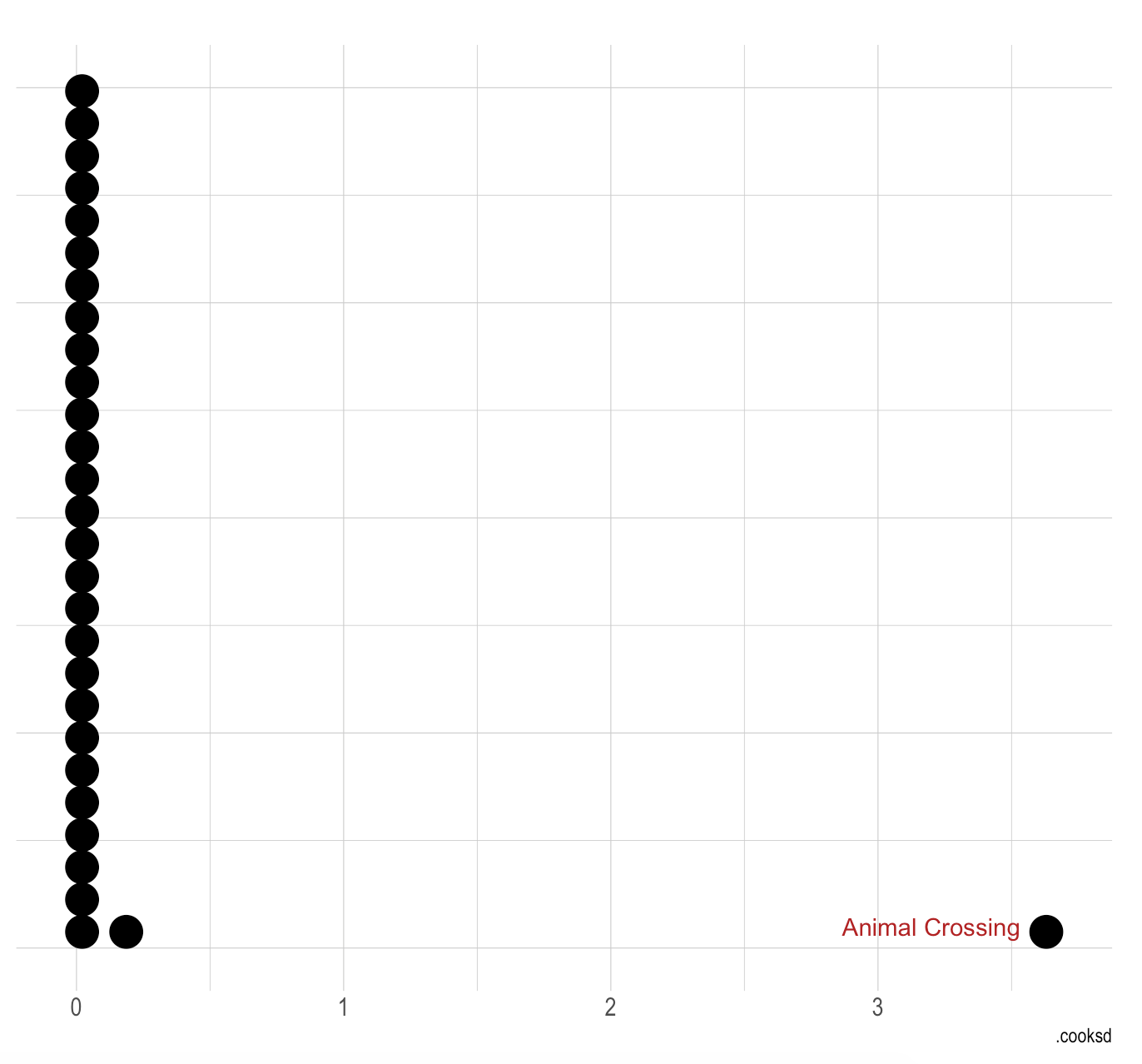
But using some domain knowledge, I’ll elect not to remove Animal Crossing from my dataset. I know there are other games with similar amounts of extra content (e.g. Stardew Valley) where the hours-to-complete soars into the hundreds. Not disqualifying for now.
And fourth: let’s see another plot:
hrs1 <- median(gametimes$hrs_to_beat)
hrs2 <- median(gametimes$hrs_to_comp)
p <- gametimes %>%
ggplot(aes(hrs_to_beat, hrs_to_comp)) +
geom_vline(xintercept = hrs1, linetype = "dashed") +
geom_hline(yintercept = hrs2, linetype = "dashed") +
geom_smooth(method = "lm", color = "red", linetype = "dashed", se = FALSE) +
geom_point() +
labs(
x = "Hrs to Beat",
y = "Hrs to Beat (Completionist)",
title = "Hours to Beat ~ Hours to Complete"
) +
theme_ipsum() +
theme(
axis.title.x = element_text(size = 12),
axis.title.y = element_text(size = 12)
)
ggMarginal(
p,
type = "boxplot",
fill = "steelblue",
outlier.alpha = 0,
size = 10
)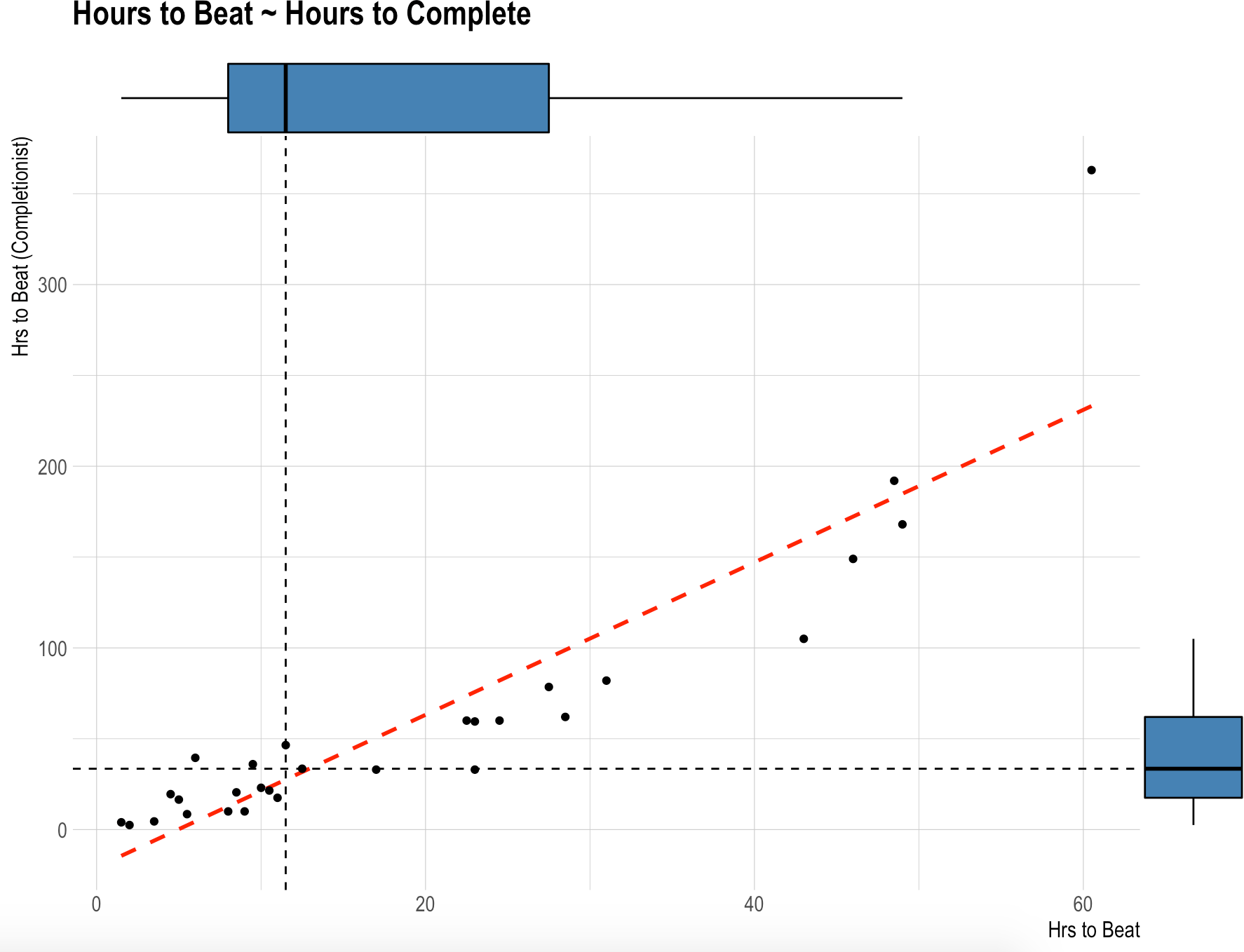
Hmmm, that doesn’t look totally linear. The fit consistently underestimates hours to complete with short games (0-10 hours), but then consistently overestimates hours to compleete with medium games (10-50 hours). Let’s venture some polynomial quadratic and cubic models instead:
qm1 <- lm(hrs_to_comp ~ poly(hrs_to_beat, 2), data = gametimes)
cm1 <- lm(hrs_to_comp ~ poly(hrs_to_beat, 3), data = gametimes)
# list(
# lm1 = lm1,
# qm1 = qm1,
# cm1 = cm1
# ) %>%
# map_dfr(glance, .id = "model")
compare_performance(lm1, qm1, cm1)# Comparison of Model Performance Indices
Name | Model | AIC | BIC | R2 | R2 (adj.) | RMSE | Sigma
----------------------------------------------------------------------
lm1 | lm | 289.296 | 293.398 | 0.817 | 0.810 | 31.992 | 33.155
qm1 | lm | 260.269 | 265.738 | 0.937 | 0.932 | 18.737 | 19.789
cm1 | lm | 234.091 | 240.927 | 0.976 | 0.973 | 11.527 | 12.415
The quadratic and cubic models unsurprisingly improve on the linear model across the board the case. Lower RMSE, higher R2, etc. The improved fits are obvious when plotted together:
gametimes %>%
ggplot(aes(hrs_to_beat, hrs_to_comp)) +
geom_point() +
geom_line(
stat = "smooth",
method = "lm",
formula = y ~ x,
linetype = "dashed",
color = "firebrick",
se = FALSE,
alpha = 0.7
) +
geom_smooth(
method = "lm",
formula = y ~ poly(x, 2),
color = "orange",
se = FALSE,
) +
geom_smooth(
method = "lm",
formula = y ~ poly(x, 3),
color = "steelblue",
se = FALSE,
) +
labs(
x = "Hours to Beat",
y = "Hours to Complete",
title = "Hours to Beat ~ Hours to Complete",
subtitle = "<span style = 'color:firebrick;'> Linear</span> and <span style = 'color:orange;'>Quadratic</span> and <span style = 'color:steelblue;'>Cubic</span> Fits"
) +
hrbrthemes::theme_ipsum() +
theme(
axis.title.x = element_text(size = 12),
axis.title.y = element_text(size = 12),
plot.subtitle = element_textbox_simple()
)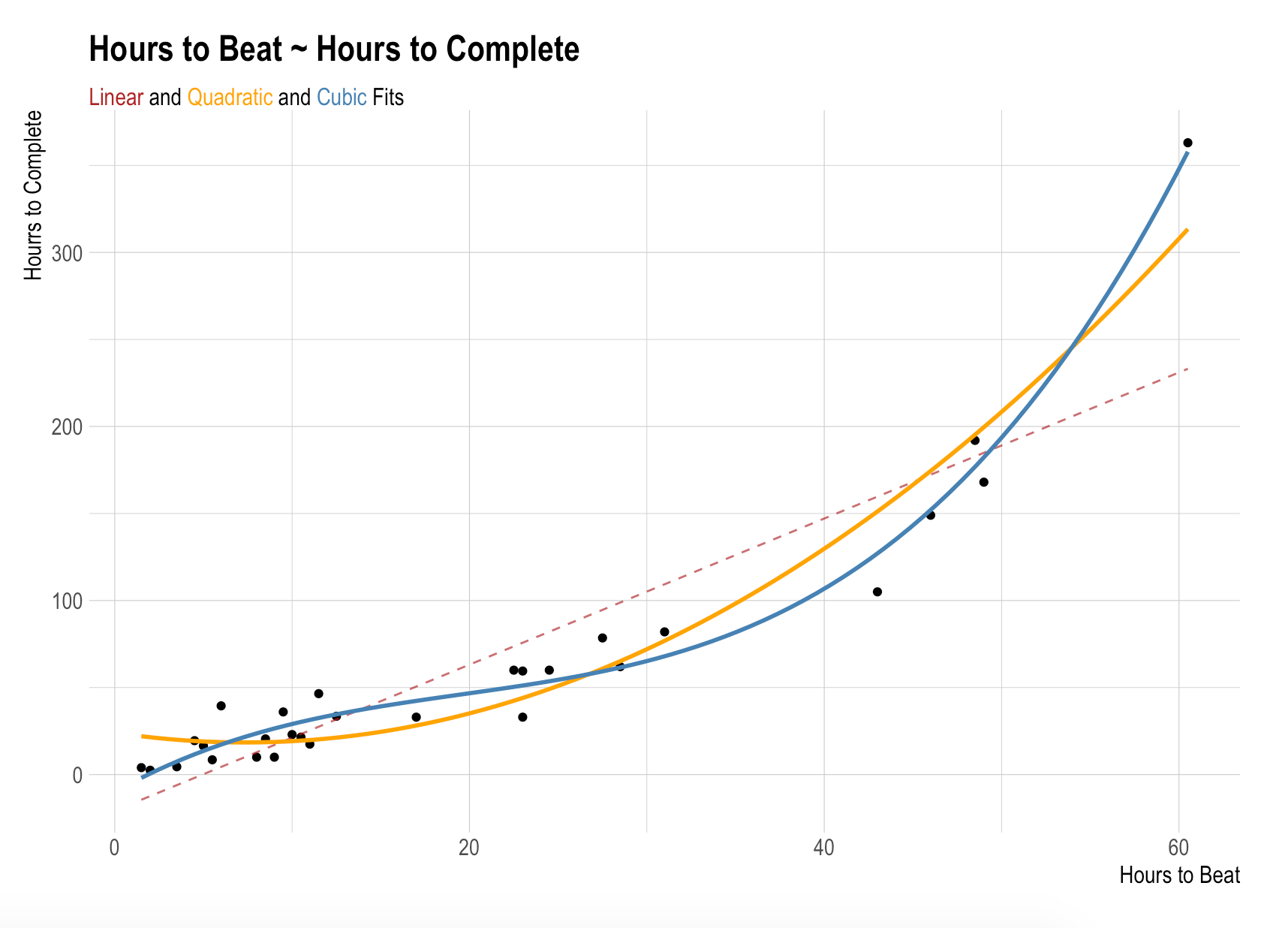
But is this classic overfitting? Let’s test the models on some new data. I unscientifically researched the hours-to-beat from some popular games I’ve played and predicted the hours-to-complete with each model. Which comes out ahead?
pred_df <- tribble(
~name, ~hrs_to_beat, ~hrs_to_comp,
"Dead Cells", 14, 85,
"Witcher 3", 51, 172,
"GRIS", 3, 6,
"Flower", 2, 5,
"Dragon Age", 40, 86,
"Control", 12, 26,
"Katamari Damacy", 5, 11,
"God of War", 21, 51,
"Disco Elysium", 20, 42,
"Final Fantasy 7 Remake", 34, 85,
"Assassin's Creed: Black Flag", 23, 59,
"Portal 2", 8, 20,
"Hades", 21, 96,
"Mass Effect 2", 25, 50,
"Sekiro: Shadows Die Twice", 29, 70,
"Pillars of Eternity II: Deadfire", 42, 90,
"Guitar Hero III", 9, 25
)
list(
lm1 = lm1,
qm1 = qm1,
cm1 = cm1
) %>%
map_dfc(~predict(.x, newdata = pred_df), .id = "model") %>%
bind_cols(pred_df) %>%
mutate(across(c(lm1, cm1), ~hrs_to_comp - .x)) %>%
rename_with(~paste0(.x, "_residuals"), .cols = matches("[lqc]m1")) %>%
select(name, matches("^hrs"), everything()) %>%
arrange(name) %>%
gt(rowname_col = "name") %>%
data_color(
columns = ends_with("residuals"),
colors = scales::col_numeric(
palette = c("firebrick", "white", "firebrick"),
domain = c(-218, 218)
)
) %>%
cols_label(
hrs_to_beat = "To Beat",
hrs_to_comp = "To Complete",
lm1_residuals = "Linear",
qm1_residuals = "Quadratic",
cm1_residuals = "Cubic"
) %>%
tab_spanner(
"Model Residuals",
columns = ends_with("residuals")
) %>%
fmt_number(
columns = ends_with("residuals"),
decimals = 1
) %>%
tab_stubhead("Game") %>%
tab_header("Predicted Hours to Complete", "Miscellaneous Video Games")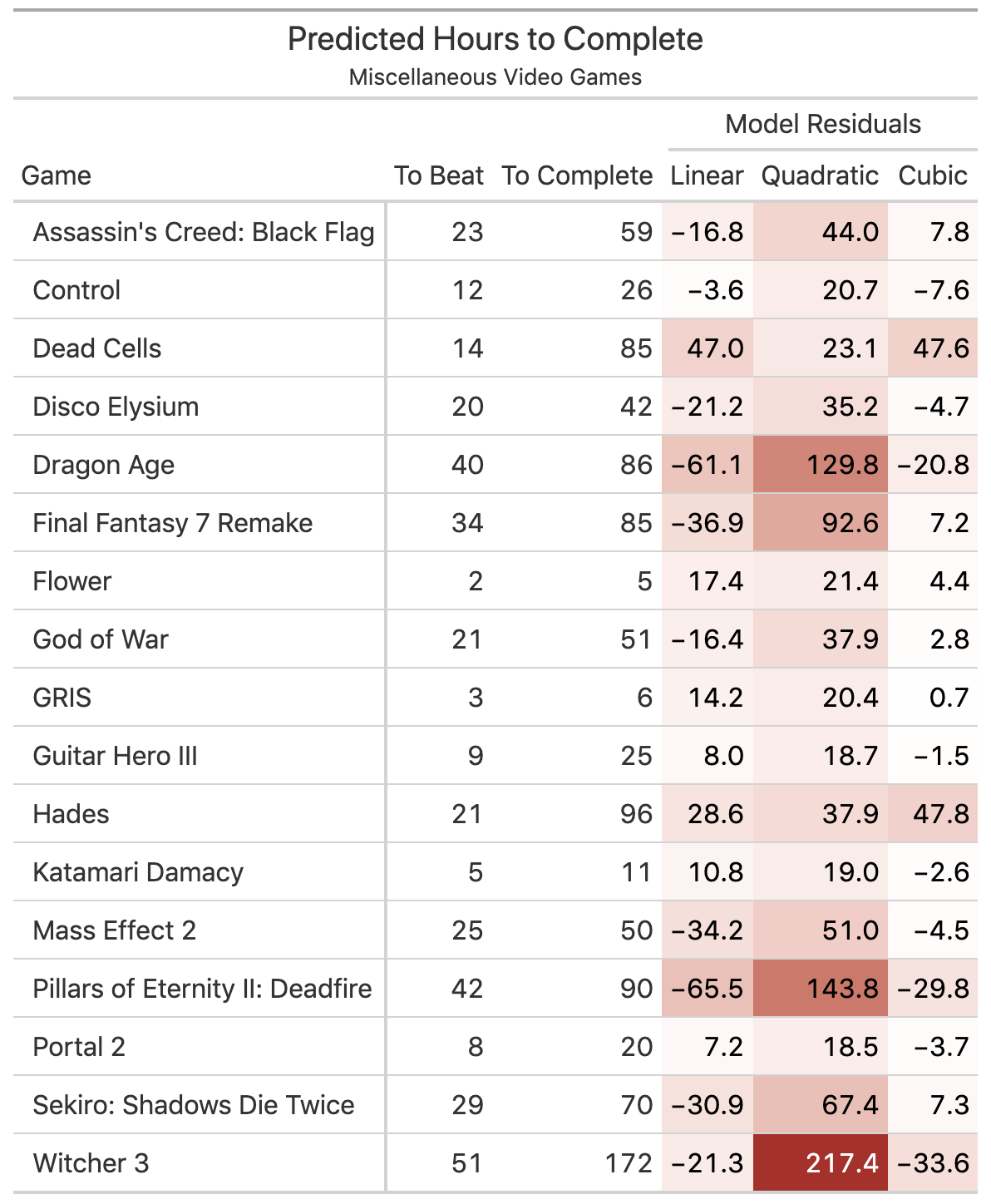
None do particularly well. The assumption of homoscedasticity appears to be violated. But the cubic model does best with short and medium length games and does a better job capturing how completion times initially scale upwards. One could perhaps coerce the y-intercept of the linear model to zero for some improvement, but that strategy is generally inadvisable.
In sum, I actually think the cubic model is capturing something real: there’s a non-linear rate to how bigger games get bigger in terms of hours to beat vs. hours to complete. There are–at a glance–three suggestive clusters: small games, medium games, and large games; and the lines of demarcation between them is not on a single slope. Whether that phenomena is due to small sample sizes, studio budgeting, genre, or creation date remains a mystery.