One of my friends is a terrible liar. The tells are numerous–irregular breathing, irrepressible grins, and pinkened cheeks. This puts him at a competitive disadvantage while playing certain table games that require an element of deception.
For example, six of us recently played the popular Cheat/BS/I doubt it.
I won’t go over the mechanics here, but it wasn’t long before the bad liar wondered aloud: ‘What are the chances that I wouldn’t have to lie and still win the game?’ My blogging antennae perked up immediately, and I announced that we could run a simulation and even brag blog about it later. Another friend scoffed and expressed disbelief (whether through ignorance or malice I do not know), and the challenge was set.
First, we create the deck and specify a function to receive a hand. 52 is not divisible by six, so if you’re playing with six people, there’s a 67% chance you receive eight cards and a 33% chance you receive nine cards. And because you can lay down any number of cards in a sequence (e.g. two “fours”, three “kings”, etc.), only the unique card values are important.
# In this deck, 'Jacks' are 11, 'Queens' 12, etc.
card_values <- rep(2:14, 4)
suits <- rep(c("H", "C", "S", "D"), each = 13)
deck <- paste0(card_values, suits)
receive_cards <- function() {
nCards <- ifelse(sample(c(TRUE, FALSE), 1, prob = c(0.67, 0.33)), 9, 8)
cards <- sample(deck, nCards, replace = FALSE)
unique(sort(as.numeric(gsub("[A-Z]$", "", cards))))
}Second, we generate the six possible sequences you would have to lay your cards down. If you start, you must first ‘play’ twos, then eights, then Aces, then sevens. If you are second, threes, nines, twos, etc:
sequences <- rep(2:14, times = 10)
six_player_sequences <- list()
for (i in 1:6) {
six_player_sequences[[i]] <- sequences[seq(i, length(sequences), 6)]
}
receive_sequence <- function() {
ind <- sample(1:6, 1)
six_player_sequences[[ind]]
}
six_player_sequences
[[1]]
[1] 2 8 14 7 13 6 12 5 11 4 10 3 9 2 8 14 7 13 6 12 5 11
[[2]]
[1] 3 9 2 8 14 7 13 6 12 5 11 4 10 3 9 2 8 14 7 13 6 12
[[3]]
[1] 4 10 3 9 2 8 14 7 13 6 12 5 11 4 10 3 9 2 8 14 7 13
[[4]]
[1] 5 11 4 10 3 9 2 8 14 7 13 6 12 5 11 4 10 3 9 2 8 14
[[5]]
[1] 6 12 5 11 4 10 3 9 2 8 14 7 13 6 12 5 11 4 10 3 9
[[6]]
[1] 7 13 6 12 5 11 4 10 3 9 2 8 14 7 13 6 12 5 11 4 10Finally, we create a function play_bs_without_lying that returns a boolean value: if every
card in your hand matches the sequence, you could hypothetically play the entire match without fibbing.
play_bs_without_lying <- function() {
cards <- receive_cards()
s <- receive_sequence()[1:length(cards)]
all(cards %in% s)
}
play_bs_without_lying()
[1] FALSENow we simulate 10000 games 1000 times and plot the distribution:
simulate_games <- function(times) {
games <- vector(mode = "logical", length = times)
for (i in seq_along(games)) {
games[i] <- play_bs_without_lying()
}
sum(games)
}
truth_games <- replicate(1000, simulate_games(10000))
# beepr::beep(3)
ggplot(as.data.frame(truth_games), aes(truth_games)) +
geom_histogram(bins = 18, fill = "lightgreen", color = "black") +
geom_vline(xintercept = mean(truth_games), color = "red", linetype = "dashed") +
annotate("text", x = 9.5, y = 145, label = "Mean: 7 Games", color = "red") +
labs(x = "Games Played without BSing",
y = "",
title = "Calling Bullsh*t",
subtitle = "Mean games without lying (10,000 games played)") +
hrbrthemes::theme_ipsum() +
theme(plot.title = element_text(face = "italic")) 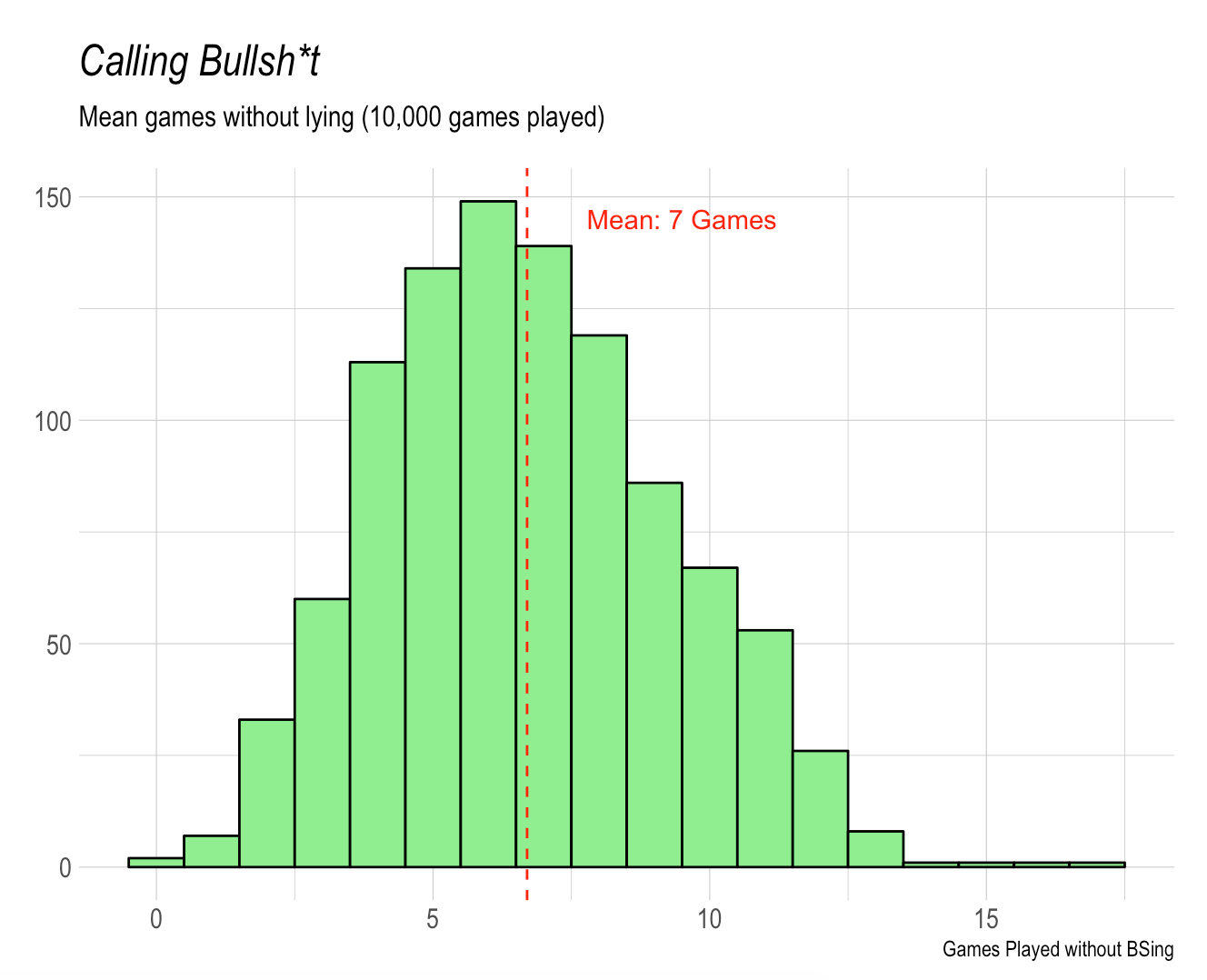
So to all the bad liars out there: if you play 10,000 games of BS/Cheat, you could expect to win without lying about seven times, or 0.0007 percent of the time.